Macam-macam Simetri pada Bangun Datar

Untuk materi pada kesempatan kali ini yang akan segera dibahas adalah mengenai macam-macam simetri pada bangun datar. Materi ini begitu mudah untuk dipahami karena kita hanya perlu menggunakan logika pemikiran saja untuk mengerti tentang simetri apa yang ada atau dimiliki oleh sebuah bangun datar. Mari kita simak langsung penjelasan materinya berikut ini:

Pengertian Macam-macam Simetri pada Bangun Datar

Simetri Putar

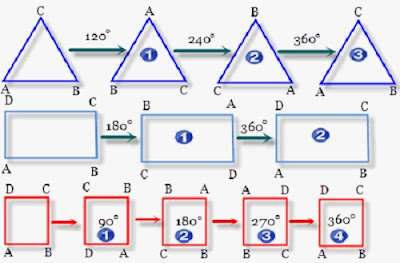
Sebuah bangun datar dapat dikatakan memiliki simetri putar apabila ia memiliki sebuah titik pusat dan apabila bangun datar tersebut dapat kita putar kurang dari satu putaran penuh untuk mendapatkan bayangan yang tepat seperti bangun semula. Sebagai contoh coba kalian perhatikan gambar berikut ini:

Pengertian dan Macam-macam Simetri pada Bangun Datar

Pada gambar di atas, ada sebuah bangun datar berbentuk segitiga sama sisi. Jika kita memutar segitiga tersebut sebanyak 1/3 putaran berlawanan ara jarum jam, maka bentuknya akan tetap sama seperti semula. Kemudian jika kita memutar segitiga sama sisi tersebut sebanyak 2/3 putaran hasil bayangannya tetap sama persis dengan bangun semula. Itu artinya segitiga sama sisi memiliki 3 simetri putar.

Apabila kita memutar sebuah bangun datar dan hanya bisa mendapatkan bayangan seperti bangun semula dalam 1 putaran penuh, artinya bangun datar tersebut tidak memiliki simetri putar sama sekali. Contohnya adalah trapesium, bangun datar ini tidak memiliki simetri putar karena kita harus memutar sebanyak 1 putaran penuh untuk memperoleh bentuk bayangan trapesium seperti bentuk bangun semula.

Tidak semua bangun datar memiliki simetri putar dan simetri lipat. Beberapa bangun datar ada yang hanya memiliki simetri putar, sementara yang lain ada yang hanya memiliki simetri lipat. Kalian bisa melihat daftar simetri lipat dan simetri putar yang dimiliki oleh tiap-tiap bangun datar pada tabel berikut ini:

Simetri Lipat

Simetri lipat pada bangun datar bisa didefinisikan sebagai banyaknya lipatan pada bangun datar yang bisa membagi bangun datar tersebut sehingga setengah bagian dari bangun datar tersebut bisa menutupi setengah bagian yang lain. Garis yang dapat membagi sebuah bangun datar menjadi dua dan kongruen disebut sebagai sumbu simetri. Perlu kalian ketahui bahwasannya tidak setiap bangun datar memiliki garis yang dinamakan sebagai sumbu simetri. Ada beberapa bangun datar yang tidak memiliki sumbu simetri sama sekali. Kalian bisa melihat beberapa bangun datar yang memiliki sumbu simetri pada gambar berikut.

Lihat gambar di atas garis atau sumbu simetri digambarkan dengan garis putus-putus. Jika anda melipat atau memotong sebuah bangun datar dengan mengikuti garis-garis simetri tersebut maka bangun datar itu akan terbagi menjadi dua bagian yang sama besar.

Nama Bangun Datar	Simetri Lipat	Simetri Putar	Sumbu Simetri
Persegi	4	4	4
Persegi Panjang	2	2	2
Belah Ketupat	2	2	2
Jajar Genjang	-	2	-
Segitiga Sama Kaki	1	-	1
Segitiga Sama Sisi	3	3	3
Segitiga Sembarang	-	-	-
Segitiga Siku-siku	1	-	1
Trapesium Sama Kaki	1	-	1
Trapesium Siku-siku	-	-	-
Trapesium Sembarang	-	-	-
Layang-layang	1	-	1
Lingkaran	Tak hingga	Tak hingga	Tak hingga

Itu saja yang dapat kami sajikan kepada anda tentang Rumus Matematika Dasar seputar Pengertian dan Macam-macam Simetri pada Bangun Datar. Kami berharap semoga kalian bisa menyerap pengetahuan dan pemahaman tentang apa yang telah dijelaskan di atas.